Modèle d'impact¶
Algorithme de détection d'impact¶
Une première version de l’algorithme de détection d’impact sur nuages de points avait été présentée lors du 12th International Symposium on Landslides – ISL 2016 :
Cette ancienne version était dépendante de l’orientation de surface du terrain. Cela la rendait plutôt sensible au bruit et aux artéfacts présents dans les nuages de points utilisés, et engendrait des résultats différents selon le rayon et la méthode utilisée pour déterminer l’orientation des terrains. Aussi, le modèle d’impact qui avait été combiné à l’algorithme pour le tester était alors basé sur les équations de la thèse de Wyllie C. Duncan (2014), contrairement aux modèles d’impacts experimentaux de la version actuelle de stnParabel.
La description de la nouvelle version de l’algorithme de détection d’impact (2021) ainsi que la description de certains modèles de rebonds existants intégrés à stnParabel aux fins de validations sont disponibles en libre accès dans :

Représentation de la forme des blocs simplifiée avec rotation autour de l'axe d3.¶
L’algorithme actuel n’utilise pas les orientations de surfaces du terrain déterminées à la section « terrain ». Celles-ci ne sont utilisées que pour la définition des sources multiples en fonction des seuils de pentes ou des tests cinématiques, et pour l’ajout facultatif des rugosités de terrain et matériaux en fonction des seuils de pente. Son fonctionnement est relativement simple, ce qui permet une simulation plutôt rapide des chutes de pierres en considérant un niveau de détail élevé du terrain. La forme du bloc est simplifiée à celle d’une sphère de diamètre d1 pour la recherche des contacts avec le terrain, les arbres ou autres éléments, et à un ellipsoïde de diamètres d1-d2-d3 tournant autour de l’axe d3 lors des rebonds.
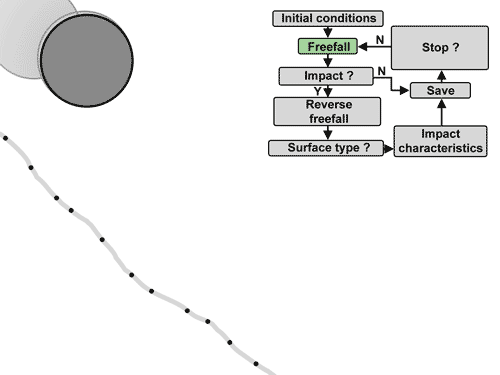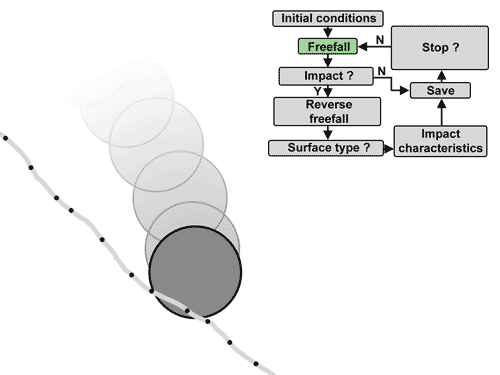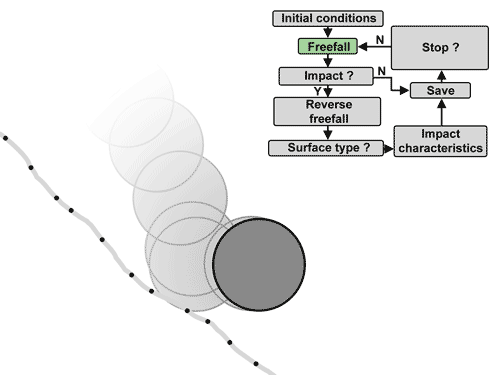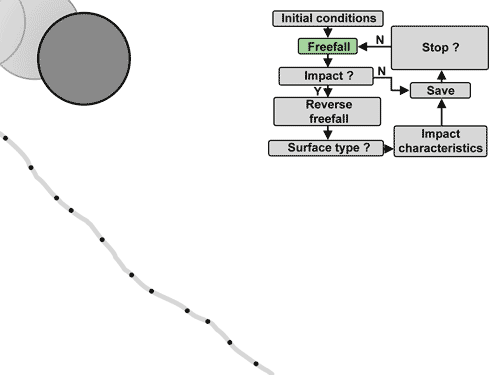
Fonctionnement simplifié de l'algorithme de détection d'impact.¶
L’algorithme consiste à déplacer l’impactant en chute libre avec résistance de l’air. La traînée est déterminée en utilisant la loi de Rayleigh avec une masse volumique de l’air de 1.2 kg/m3, une surface de référence de l’impactant vu de face sous forme d’ellipse aux diamètres d1-d3 et un coefficient de traînée de 0.9. Puis de vérifier si des points sont impactés après chaque distance parcourue de 70 à 85% du diamètre maximal d1. Si c’est le cas, plusieurs options sont possibles :
Si un filet est impacté, l’impactant est arrêté et la trajectoire est enregistrée;
Si une infrastructure est impactée, les informations du premier impact de ce type par trajectoire sont enregistrées et la chute libre se poursuit;
Si le terrain ou un tronc est impacté, la chute libre précédente est inversée (le temps est négatif) jusqu’à trouver la position précise d’impact tangente aux points, ou tangente à la surface des troncs d’arbres coniques. Pour le rebond contre le tronc, le modèle d’impact est ensuite appliqué (voir la sous-section « Modèle d’impact contre les troncs).
S’il y a impact contre le terrain, Les points du terrain autour du point impacté sont alors isolés dans un rayon de ½ d1 et un plan leur est ajusté. Si le plan correspond bien aux points (RMS < 0.04*d1), et donc que le terrain est localement lisse, l’impactant est déplacé en chute libre inversée jusqu’à être tangent au plan et l’orientation du terrain perçue par l’impactant est donnée par celle du plan. Sinon, l’orientation du terrain perçue est donnée par le vecteur normé partant du point impacté et pointant vers le centre de masse de l’impactant. Le modèle d’impact est ensuite appliqué pour le rebond (voir la sous-section « Modèles d’impact contre les terrains).
Modèle d'impact contre les troncs¶
Le modèle d’impact contre les troncs reprend les équations utilisées dans Rockyfor3D v5.2, basées principalement sur les travaux de Luuc Dorren et Frédérique Berger et testées dans la thèse de Martin Jonsson (2007) et est décrit en détail dans :
La déviation latérale qui survient après un impact contre un tronc se base sur les déviations probabilistes (θRF3D) utilisées dans Rockyfor3D v5.2. Elle est cependant ajustée à la baisse arbitrairement en fonction du changement de vitesse (RV_tree = Vout/Vin) occasionné par l’impact contre le tronc tel que suit : θstnParabel = θRF3D*(1-RV_tree3). Cette modification fait en sorte que les impacts à forte énergie contre de petits troncs, où le bloc ne perd que peu d’énergie, ne peuvent être que légèrement déviés (ex. : θstnParabel = ~99% de θRF3D pour un RV_tree de 0.2, ~88% pour 0.5, ~27% pour 0.9 et ~3% pour 0.99).
Modèle d'impact contre les barrières¶
stnParabel v.June 2021 ne considère pas la déformation des filets et murs ni leur capacité à résister à l’impact. Le modèle d’impact contre les terrains est utilisé pour les murs. Aussi, les blocs sont arrêtés dès qu’ils touchent le filet, que leur centre de masse se situent à l’intérieur des limites du filet ou au-delà, et peu importe l’énergie à l’impact. Il peut donc être nécessaire de réduire légèrement la hauteur des filets d’un demi-diamètre (½ d1) des blocs pour les simulations.
Modèles d'impact contre les terrains¶
La fragmentation des blocs n’est actuellement pas prise en compte lors des impacts contre les terrains. Différents modèles d’impacts existants ont été testés, combinés à l’algorithme de détection d’impacts sur nuages de points original à stnParabel. Certains de ces anciens modèles se basent sur Pfeiffer et Bowen (1989), et donc sur des coefficients de restitution COR fonctions de Rt, Rn, Rg10, Rg20, Rg70, soiltype, l’angle d’impact, etc., pour déterminer la perte d’énergie instantanée qui survient aux impacts (le temps de contact est négligé). Le choix des différents facteurs permettant de déterminer les COR peut cependant introduire un large biais, car ces facteurs sont souvent difficiles à mesurer sur le terrain et propres à chaque logiciel. Certains de ces modèles peuvent tout de même être utilisés dans stnParabel.
D’autres modèles d’impacts tiennent compte d’une durée de contact pendant laquelle la vitesse de l’impactant évolue en fonction des différentes forces dues au contact. Le bloc est généralement considéré comme un corps rigide. Les surfaces impactées ont en général une certaine tolérance à l’enfoncement afin d’éviter un contact rigide-rigide. Un tel contact autrement engendrerait des forces infinies lors des impacts et des temps de contact nulles, complexifiant l’application des forces de frottement. Les forces de frottement sont souvent définies selon Coulomb / Mohr-Coulomb. Les modèles d’impact Rolling friction et Scarring model développés pour stnParabel utilisent ce type d’approche pour déterminer l’évolution des vitesses de rotation et de translation du bloc. Ils utilisent ensuite des relations empiriques basées sur des expériences de chutes de blocs pour appliquer les déviations latérales et verticales.
Les déviations « latérales » sont appliquées par une rotation autour d’un axe passant par le centre de masse du bloc et perpendiculaire au terrain perçu. Les déviations « verticales » sont appliquées par une rotation autour d’un axe passant par le centre de masse du bloc et perpendiculaire à l’axe précédent. Elles sont définies de façon à satisfaire au mieux des relations empiriques établies après la mesure 3D de près de 500 impacts réels, allant de quelques kilojoules à quelques centaines de mégajoules. La forme et l’inertie des blocs étudiés a été mesurée précisément à partir de modèles 3D et de pesées de terrain ou d’échantillonnage pour la masse volumique des deux blocs au-delà de 180m3. Ces relations utilisent entre autres les changements de vitesses en [X, Y, Z] et de rotation, l’allongement du bloc selon le ratio d2/d1, l’aplatissement du bloc selon le ratio d3/d1, l’angle incident avec le terrain perçu, la différence d’orientation du terrain par rapport à la direction du bloc avant l’impact, etc.
Les deux nouveaux modèles permettant de déterminer les changements de vitesses sont rapidement décrits aux sous-sections suivantes afin d’en donner un aperçu en attendant la publication de la description détaillée de leur fonctionnement. Les deux utilisent la masse entrée via l’interface de stnParabel et l’inertie du bloc simplifié à un ellipsoïde tournant autour de l’axe d3 afin de déterminer les changements de vitesses.
Le premier modèle (Rolling friction model) est le plus simple à utiliser des deux, car il ne nécessite pas de définition des matériaux de terrain. Au moment d’écrire ces lignes, l’auteur l’a testé pour 8 différents sites affectés par des événements passés et obtient des trajectoires et positions d’arrêt des blocs similaires à celles observées pour 7 des 8 sites. Le modèle peine cependant à reproduire l’une des deux positions d’arrêt (celle au plus long runout) pour l’événement ayant affecté Holaviki décrit dans :
Domaas, U. (Norwegian G. I. (1995). Natural rockfalls - Descriptions and calculations.
Les chutes de pierres atteignent des vitesses impressionnantes pour ce site à cause de la haute paroi (elles dépassent en majorité les 50 m/s), et les matériaux en bas de pente ont surement une faible résistance, à cause de leur teneur en eau probablement élevée. Le second modèle peut alors être utilisé pour ces cas particuliers afin d’avoir plus de contrôle sur l’interaction entre le bloc et les matériaux de surface.
Rolling friction model¶
Ce modèle, original à stnParabel, assume un certain enfoncement du bloc dans le sol, sans toutefois le calculer en détail. Le modèle est décrit en détail dans:
L’accélération dans le sens de la normale au terrain (αN) est simplifiée à une valeur constante. Cela permet d’obtenir la force normale au terrain qui s’applique sur un intervalle de temps (δT) pendant lequel le bloc s’enfonce dans le terrain et en ressort. Ce temps de contact est défini par le temps (δT_decel) nécessaire pour que le bloc ait une vitesse normale au terrain (VN) nulle, auquel s’ajoute un court laps de temps (δT_accel) nécessaire pour que cette vitesse lui permette de s’éloigner à nouveau du terrain.
Pendant ce temps δT ou jusqu’à ce que la vitesse de rotation (VRot) du bloc se synchronise à sa vitesse de translation (VT), une force de frottement est appliquée en utilisant la force normale au terrain en fonction de Mohr-Coulomb, affectant VT et VRot. La direction de cette force est parallèle au terrain et fonction du glissement ou du dérapage du bloc (skidding ou slipping). Si la rotation se synchronise, une simple résistance au roulement est appliquée jusqu’à la fin du contact avec un coefficient de résistance au roulement (bRot) fonction de VT_in et de ½ d1. Une limite arbitraire empêche le bloc de décélérer de plus de 90% de sa vitesse initiale lors de l'impact.
Les propriétés des matériaux sont fixées à un φ’ de 28° et à une cohésion de 30 kPa pour ce modèle (puisque le cisaillement sous l’impactant ne se produit pas qu’à l’interface bloc-sol mais aussi légèrement au travers du sol). Ces valeurs ont été choisies afin d’obtenir les meilleurs R2 lors de la comparaison du modèle à la base de données d’impact (près de 500 impacts, de quelques kilojoules à quelques centaines de mégajoules). Cette comparaison a été automatisée afin de tester des milliers de combinaisons de paramètres et de choisir ceux permettant de reproduire au mieux les vitesses restituées (tangentielles, rotation, angles de déviation, etc.).
Scarring model¶
Ce modèle expérimental, original à stnParabel, calcule l’enfoncement du bloc dans le terrain en fonction de la capacité portante du sol pour les propriétés des matériaux définies localement par rapport aux seuils de pente. La portance dynamique créée par la projection du sol au front du bloc y est aussi combinée jusqu’à ce que le bloc atteigne son enfoncement maximal (lorsque VN change de signe). Cette portance dynamique agit ensuite seule sur le bloc jusqu’à la fin du contact. La cohésion n’est appliquée que pour la capacité portante du sol, et non sur la portion dynamique du sol projeté à l’avant ni sur le frottement entre le bloc et le sol.